Post by J.FPost by WMPost by WMZ okazji Międzynarodowego Dnia Pszczół, przygotowałem zagadkę z cyklu - znajdź różnice w obrazkach.
https://images92.fotosik.pl/665/bba653256b38000cmed.png
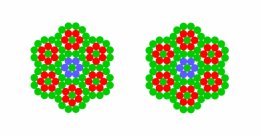
Środki okręgów tworzą wielokąty foremne.
Pozornie wygląda tak, jakby każde czerwone 6 kółek otaczał zielony kółkowy sześciokąt foremny.
W rzeczywistości otacza je dwunastokąt foremny, co trudno zauważyć z powodu podobieństwa całej zielonej części do plastra miodu.
W dwunastokącie, sześciokąt może przyjąć dwie rozróżnialne pozycje: wierzchołkiem do góry i wierzchołkiem w bok.
No i po zrobieniu zeza to od razu widac.
Dookołą jednego kółka mozna ułożyc 6 takich samych kółek, i będą one
scisle przylegac do siebie.
Ale czy dookola tych 6 da sie ułożyc 12? tego samego promienia czy
innego? Będą scisle przylegac do siebie, czy z luzem?
Bedą srodki tworzyc wielokąt foremny, czy wcale nie foremny, tylko
jakos 6 katow takich samych, a druga 6 innech.
Patrze na to ... odpowiednie pary z tych 12 sa translacja pary z
wewnetrznej 6, co gwarantuje styk miedzy nimi przy tym samym
promieniu. I chyba styk pomiedzy parami. To i odległosci między
srodkami. Więc chyba i foremnosc?
Post by WMChcę umieścić kulki z jednego obrazka, wewnątrz okrągłej komory z pewnym małym luzem.
Luz ma ułatwić obrót jednego zestawu sześciu kulek, między dwoma pozycjami.
Nie wiem tylko czy ten luz nie spowoduje czasem przejścia układu kulek w kompletny chaos.
Czyli cos w rodzaju lożyska tocznego chcesz zrobic?
Nie da się zrobić z tego łożyska.